円錐とそれに内接する球の表面積比と体積比について 球が内接する立体とその内接球について,体積比と表面積比が等しい。 404 円錐とそれに内接する球の表面積比と体積比について – GeoGebra Materials 一覧へ戻る 計算公式円錐の体積の求め方がわかる3つのステップ 円錐の体積の求め方の公式って?? こんにちは、この記事をかいているKenだよ。犬の散歩が趣味だね。 円錐の体積の求め方の公式は、 底面積×高さ×1/3 だったよね。 もう少し詳しくかいてあげると、第6章 立体図形 と 比 の最新傾向・学習方法 1テーマの意味 立体図形と比 立体図形も、5年生中盤までに、具体量を使って、「長さを求めさせる問題」、「体積を求めさせる問題」などを一旦学習します。 その後、「比」を学習した後、先ほどの
体積比と相似 立体図形で相似比a Bなら体積比は A A A B B B 中学受験 塾なし の勉強法
円柱 円錐 体積比
円柱 円錐 体積比-円錐と内接球・その1の追加問題です。 問題1と完全に同じ求め方により、 21cm 21 c m と求まります。 ここまで求めた状態から、次に上の小さい球の半径を求めます。 下の図のようになっています。 下図の水色の直角三角形も 3 3 辺の比が 25 24 7 25 24 7(1) と の表面積の比を求めよ。 (2) と の体積の比を求めよ。 例題 解答 (1) 円錐 と円錐 の相似比は底面の半径の比なので, よって,表面積の比は (2) 円錐 と円錐 の相似比は底面の半径の比なので, よって,体積の比は
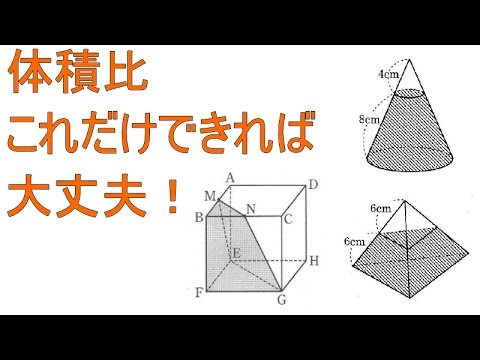



相似比と体積の計算 円錐台 三角錐台 中学3年数学 Youtube
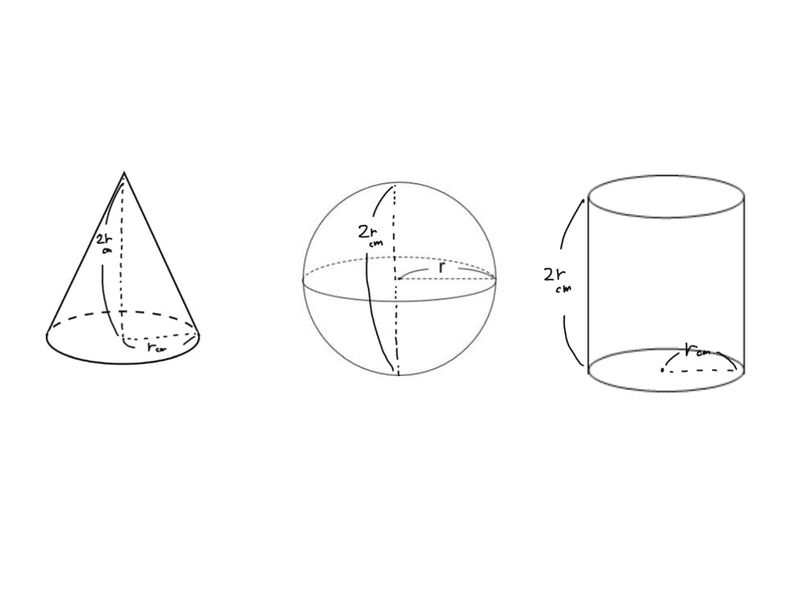
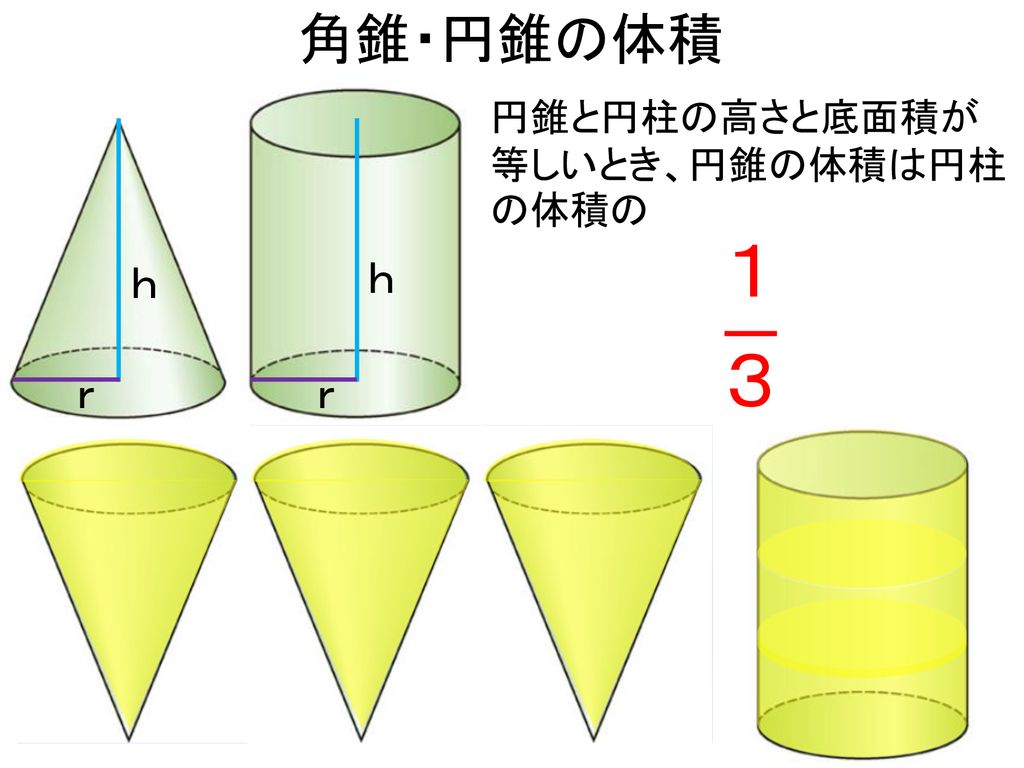
各々の体積の求め方は知ってはいるのですが、意外に体積比を知らない 円柱と球と円錐の関係 数学・化学講師 佐藤学による受験生に役立つ濃縮ポイントとetc ホーム ピグ アメブロ 芸能人ブログ 人気ブログ Ameba新規登録(無料) ログイン 数学・化学講師 佐藤学による受験生に役立つ円柱と円錐と球の体積 底面の直径が5cmで高さが5cmの円柱と円錐があります。さらに,直径が5cmの球があります。 体積比はどうなるでしょう。 円柱の体積は V1 = πr2 ×2r = 2πr3 円錐の体積は V2 = 2πr3 × 3 1 = 3 2 πr3 球の体積は V3 = 3 2 π r 3 ×2 = 3 4 π r 3直円錐の体積 直円錐の体積 直円錐の半径と高さから体積、側面積、表面積を計算します。 斜切円錐の体積 斜切円錐の体積 直円錐を斜めに切断した体積と切断面積と底面積を計算します。 一部が欠けた直円錐の体積 一部が欠けた直円錐の体積
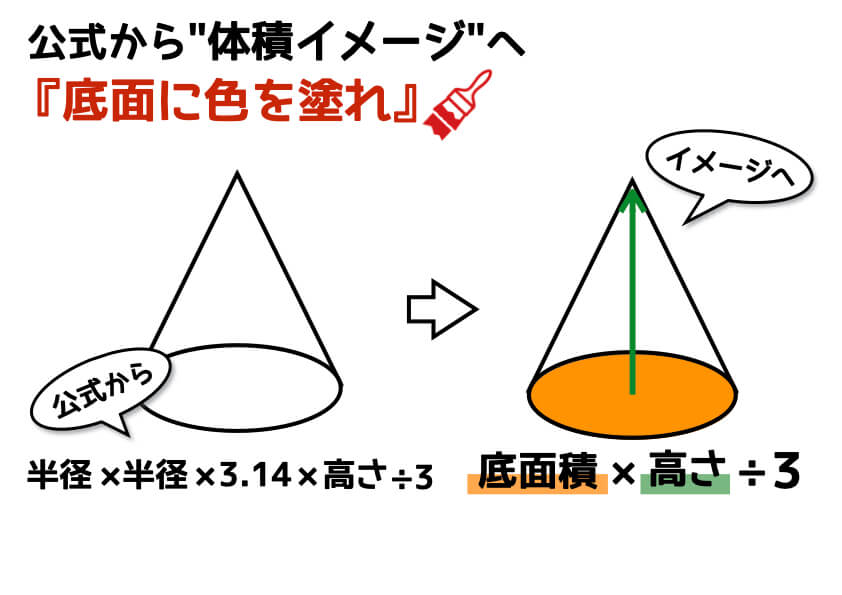
三角錐,四角錐,円錐などの錐体の体積は 1 3 \dfrac{1}{3} 3 1 ×底面積×高さ 底面積が S S S ,高さが h h h である錐体の体積 V V V を求める公式: V = 1 3 S h V=\dfrac{1}{3}Sh V = 3 1 S h の導出を紹介します。円錐を切り取って体積比を考えるような問題では 比較する立体が相似でなくても このように相似な立体を見つけて、不要な部分を取り除いたりしながら考えると答えを求めることができます。 円錐 の 側 面積 の 求め 方 ☢ 角柱や円柱とは、異なる計算方法になります。 5 そのため、母線を円錐の体積 円錐の体積は, V = 1 3πr2h V = 1 3 π r 2 h ( r r :半径, h h :高さ ) の公式で求めることができる. この公式は,円柱の体積の公式 V = πr2h V = π r 2 h に 1 3 1 3 をかけたものと考えることができるが,なぜ円柱の体積に 1 3 1 3 をかけることにより
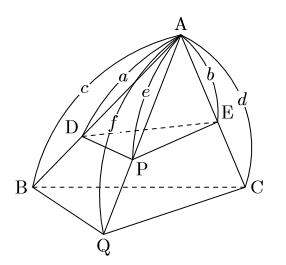
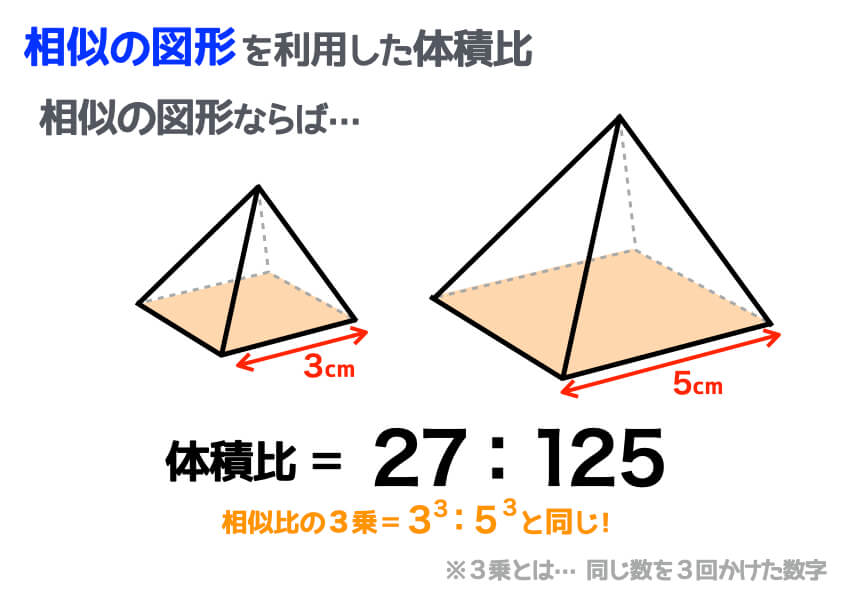
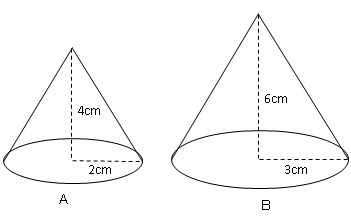
体積の比 8πr 2 h27πr 2 h=7 確認 答表示 円錐Aと円錐Bは相似で、相似比は34である。 AとBの表面積の比を求めよ。 916 AとBの体積の比を求めよ。 2764 円柱Cと円柱Dは相似で、表面積の比が925である。 円柱Cの体積が270πcm 3 のときの円柱Dの体積を求めよ。 1250πcm 3相似比→ : 面積比→ : (2) adeと四角形dbceの面積比を求めなさい。求め方が分かるようにかきなさ い。 求め方 面積の比→ : 2 円錐の形をした容器に,コップ1杯のジュースを入れたところ,容器の高さの の ところまでジュースが入りました。この容器もとの正四面体と小さい正四面体の相似比は $21$ だから、体積比は $2^31^3=81$、つまり、正四面体の体積を $V$ とすると小さい正四面体の体積は $\dfrac{V}{8}$。よって、正八面体の体積は $V4\times\left(\dfrac{V}{8}\right)=\dfrac{V}{2}$ となり、求める比は $V\dfrac{V}{2}=\boldsymbol{21}$ である。



面積比と体積比の問題です 高さが9 の円錐pがある pを下の図のように高 Yahoo 知恵袋



円錐 球 円柱の体積 雑学のソムリエ
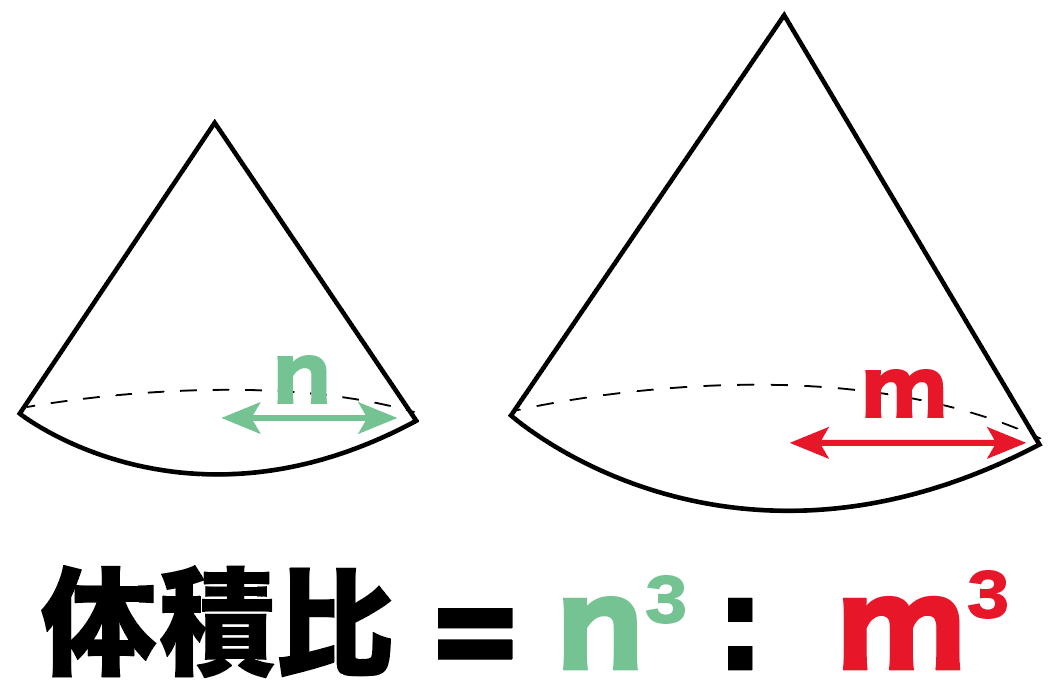
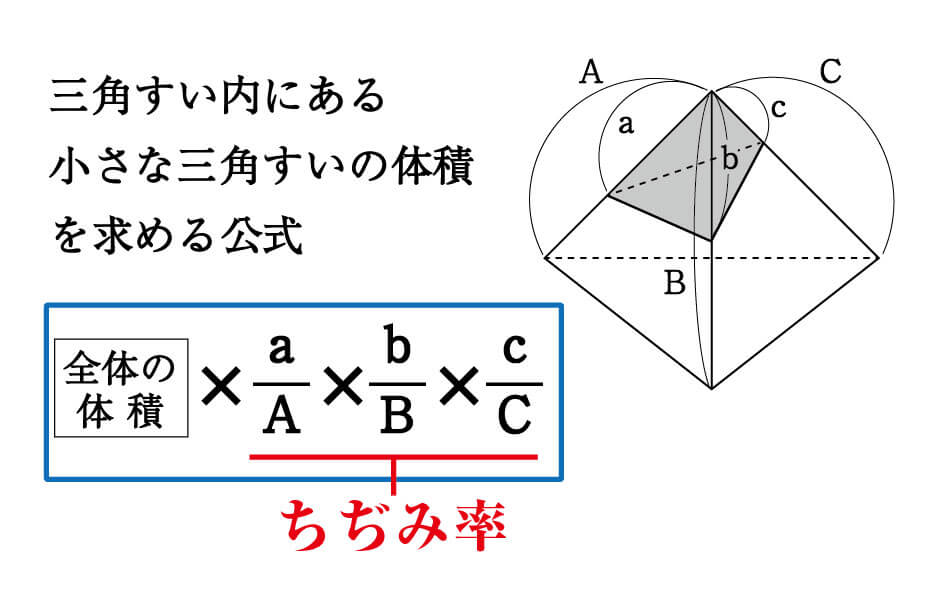
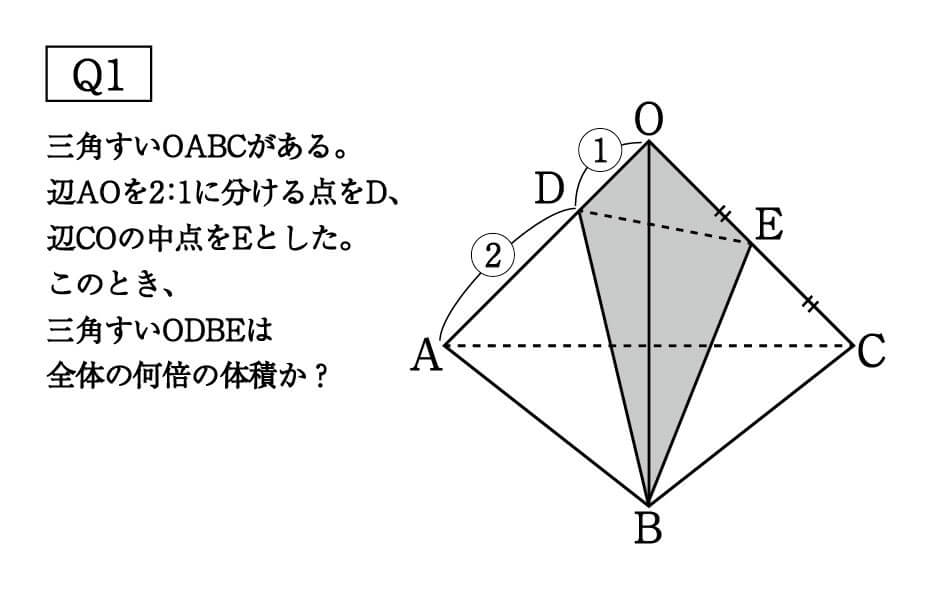
各辺の比は、次のように表すことができます。 ao:do=3:2 bo:eo=2:1 co:fo=4:1 よって、全体に対する三角すいodefのちぢみ率は、以下となります。 円錐の体積の公式は底面の円の半径をr、円錐の高さをhとすると、 (1/3)π(r^2)h となる。 次に、kを正の実数とし、相似比kの円錐を考えると、半径はk倍、高さもk倍になることから、 (1/3)π((kr)^2)kh=(1/3)(k^3)π(r^2)h となり、相似の体積比は相似比kの3乗になる。V=Sh 特に,円柱については,底面の半径が r であるとき,底面積が S=πr 2 と書けるから V=πr 2 h と書くこともできます. ※簡単なことのように見えますが,底面と高さとが直角になっている場合だけこの公式が使えます.例えば,右図において Sl はこの立体の体積ではありません. 要点四角錐,三角錐,円錐の体積 三角錐,四角錐,円錐の体積 V は,それ



Www Pref Osaka Lg Jp Attach 6629 Jmw 3b5 11 Pdf




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ
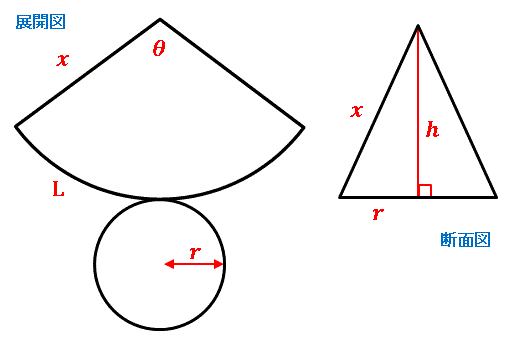
円錐は展開図にすると,円と扇形に分離されるのでこのような公式になります. 展開図がそのまま数式になっているので非常に分かりやすく理解しやすいと思います. 体積を求める公式 V = 1 3 π r 2 h V = 1 3 π r 2 h さて,次は円錐の体積を求める公式です.5.円錐台の側面積 円錐台は4の全体円錐から、上部の円錐を引けば求められる。 h,l の母線 それでは、塩水の相似比、面積比、体積比の算出に慣れるためにも、練習問題を解いていきましょう。 例題 Q 円錐の体積比 中学数学の問題です。 円錐の形をした深さが10cmの容器に水を162立方センチメートル入れたところ、 水の深さが6cmになった。 この容器をいっぱいにするには、水をあと何立方センチメートル入れればいいか。 この問題の解法がわかりません。 どなたか教えてください。




3分でわかる 相似比から体積の比 表面積比を求める公式 Qikeru 学びを楽しくわかりやすく



小学生でもスッキリ理解できる 体積比のコツと求め方 中学受験ナビ
(1)球と円柱の体積比を求めなさい。 (2)球と円柱の表面積の比を求めなさい。 半径1の球と,底面の直径と高さがともに 2である円錐について 問題1.定球の体積とその定球に外接する体積最小の直円錐の体積の比を求めよ。また、表面積の比も求めよ。 問題2.円形の紙から扇形を切り取って漏斗を作り、その容積を最大にするには切り取る中心角をいくらにすればよいか? それではよろしくお願いします。 ベストアンサー 数学円錐の体積を求める公式は、次の通りです。 V = 1 3Sh = 1 3πr2h V = 1 3 S h = 1 3 π r 2 h ここで、V は円錐の体積、S は底面積、h は高さを表します。 また、2行目における π は円周率、r は底面の円の半径です。 円錐の体積を求めるには、この公式に底面の半径 r と高さ h を代入すればよいだけです。 このページの続きでは、例題を使って、この公式の使い方を説明してい



Studydoctor相似比と体積比 円錐台 中学3年数学 Studydoctor
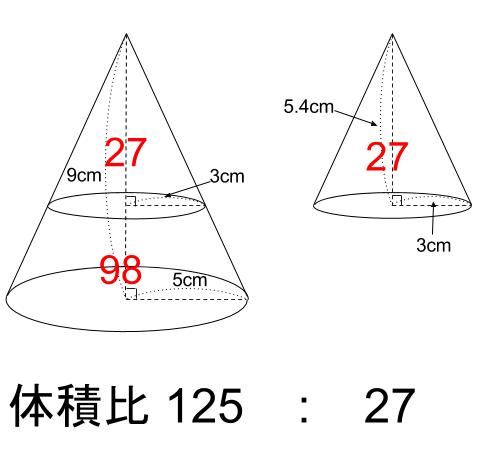



中学数学 相似な図形の体積比 中学数学の無料オンライン学習サイトchu Su
錐体(円錐、角錐)の体積は、底面積が S S 、高さが h h の錐体の体積 V V は以下の式で表します。 V = 1 3Sh V = 1 3 S h この公式を学習したときに 1 3 1 3 になる理由は知らなかったと思います。 これは特殊な四角錐の場合には比を用いて簡単に証明することが体積の求め方は、立体の形状で違います。 重量は、質量に重力加速度を掛けた値です。質量と意味が違うので注意してください。質量と重量の違いは、下記が参考になります。 質量、重量とは?1分でわかる意味、違い、換算、体重計、重力との関係 比重は下記が参考になります。 比重の単位手っ取り早く円錐の体積を求めるには、この公式に値を代入すればよいだけです。 このページの続きでは、公式の導出方法も説明していますが、公式を使わずに、順番に計算する方法もお示ししますので、みなさんの必要に応じて使い分けてください。 もくじ 円錐の表面積を求める公式 公式




相似比と体積比 円錐台 中学3年数学 Youtube



円錐 球 円柱の体積比で出くわした 数学の神秘 に付いていけなかった話 がお Note
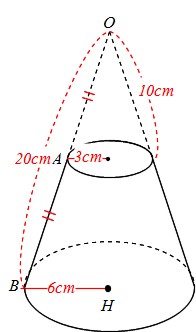
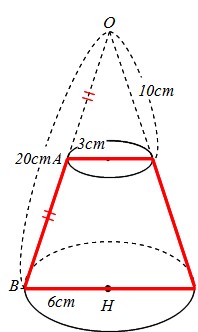
小さな円錐の母線の長さを x cmとする。 大小の円錐において、母線の長さの相似比は 8:x なので、 体積比は、8 3 :x 3 =8:1円錐や三角錐の体積比の求め方 相似比 辺の長さの比から計算 白丸くん中3_三角形の相似_円錐の体積比(日本語版) Watch later Share Info Shopping Tap to unmute If playback doesn't begin shortly, try restarting your device You're signed out Videos you watch may be added to the TV's watch history and influence TV recommendations




公式を図解 すい体の体積 円すいの表面積の求め方



Q Tbn And9gcteatlk3su2k13ppiy286tged4bmtwyxvgsndquhix Behamia0 Usqp Cau
円錐の体積ってなんであの公式なの │ Webty Staff Blog 三角錐の体積比の計算方法 今度は、三角錐において、相似比や面積比から体積比に換算する方法について解説していきます。 上の図で表したように、側面のおうぎ形の弧の長さと、底面の円の円周の長さを等しくしなければ正しく立体が 11年東工大 数学 第4問 は回転体の体積に関する問題です。正方形を軸に沿って回転させるだけなのですが、軸が正方形のどの辺とも平行でないため、計算量が爆発します。取り付く島がない系の問題とは違いますが、時間内に終わる気がしないアンタッチャブル問題です。球の体積、表面積 半径rの球 表面積=4πr 2 、 体積= 4 3 πr 3 r (例)半径6cmの円 6cm 表面積=4π×6×6=144π(cm 2) 体積= 4 3 π×6×6×6=2π(cm 3) 回転体の体積 回転体は、円錐や円柱、球などの組み合わせでできているので、 それぞれの部分で体積を出して足したり、引い



中学数学 公式 三角錐の体積比 数樂管理人のブログ



Math 円錐 円錐台と面積比 体積比 働きアリ
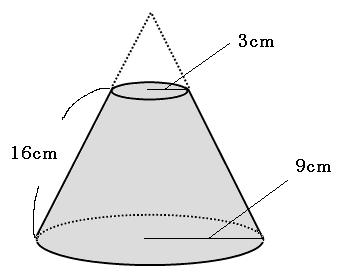
体積の公式に当てはめて $$9\pi \times 4 \times \frac{1}{3}$$ $$=12\pi cm^3$$ となります。 半径がわからない場合でも 考え方は、高さを求めるときと同じですね! 円錐の体積を求める方法 まとめ お疲れ様でした! 円錐の体積を求めるときに 高さや半径がわからこの立体の体積は (cm 3 ) 外側の体積 160π (cm3)から空洞になっている内側の体積 40π (cm3)を引くと V=1π (cm3) 大きな円錐の体積は π×6 2 ×10÷3=1π (cm3) 上端の円錐の底面の半径 ( x とおく)は,比例(相似)の関係を使って求めることができる.縦:横 x 5x=106



Www Pref Osaka Lg Jp Attach 6629 Jmw 3b5 11 Pdf



円錐と円柱の体積比 中学 数学 学習教材 実演器 Ed 0009 Cornvolumer 西条問屋 通販 Yahoo ショッピング



Math 円錐 円錐台と面積比 体積比 働きアリ




三平方の定理の利用 四角錐 円錐 チーム エン



3分でわかる 相似比から体積の比 表面積比を求める公式 Qikeru 学びを楽しくわかりやすく



小学生でもスッキリ理解できる 体積比のコツと求め方 中学受験ナビ




空間図形14 円すい台の体積 Youtube




相似比と体積の計算 円錐台 三角錐台 中学3年数学 Youtube




3分でわかる 相似比から体積の比 表面積比を求める公式 Qikeru 学びを楽しくわかりやすく



2



面積比と体積比 中学から数学だいすき



数学 三角錐の体積比を楽に求められる公式 受験の秒殺テク 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



円錐を カット する 体積は どうなる 名寄 算数数学教室より



本時の目標 いろいろな立体の体積を求めることができる Ppt Download




身近な数学 きのこたけのこの体積比 準備 測ってみてた 身近な数学 問題作り




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




立体図形の体積の証明 錐体 数学ノート




一番最後の問題がわかりません 円錐だから体積比が使えなくて困ってます Clear




円錐の体積の求め方 公式と計算例




相似比と体積の計算 円錐台 三角錐台 中学3年数学 勉強 Youtube スタディチューブ



相似と体積比 1 ネット塾




3分でわかる 相似比から体積の比 表面積比を求める公式 Qikeru 学びを楽しくわかりやすく




公式を図解 すい体の体積 円すいの表面積の求め方




3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ



Math 空間図形と相似 面積比 体積比 発展問題 働きアリ The 2nd



下の図のように 体積が144立方センチメートルの円錐を底面に平 Yahoo 知恵袋




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット



Http Happylilac Net Pdf Jhs Math3 05 03ans 04 Pdf




3d100 Descubre Como Resolverlo En Qanda




3分でわかる 相似比から体積の比 表面積比を求める公式 Qikeru 学びを楽しくわかりやすく




なんで144に8分の1をかけるんですか Clear




中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ




空間図形の表面積比と体積比 数学i フリー教材開発コミュニティ Ftext




どうして1 3なの 錐の体積の公式の求め方 まなべーと




高校数学 3辺の長さが等しい 三脚型 四面体の体積 受験の月




体積比と相似 立体図形で相似比a Bなら体積比は A A A B B B 中学受験 塾なし の勉強法
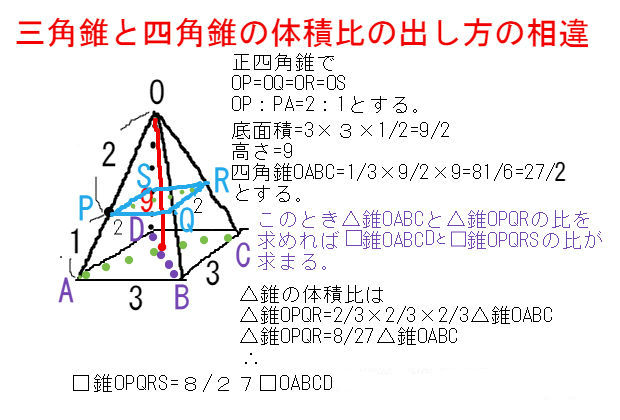



三角錐と四角錐の体積比計算方法の違い 中学数学 理科 寺子屋塾の復習サイト




相似比と体積比 円錐台 中学3年数学 勉強 Youtube スタディチューブ




勢いで丸してしまったんですが 円錐の体積ってpいらないのでしょうか Clear



立体の体積比 第1問 開成中学 まいにち一題 中学受験過去問題研究



円錐とそれに内接する球の表面積比と体積比について 久保塾 今治市の学習塾



今月の問題




図形の面積比 体積比 数学i フリー教材開発コミュニティ Ftext



Studydoctor相似比と体積の計算 円錐台 三角錐台 中学3年数学 Studydoctor
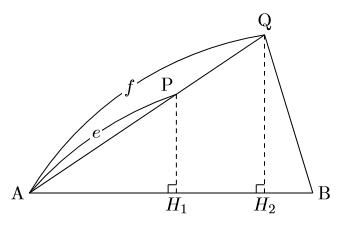



中学数学 公式 三角錐の体積比 数樂管理人のブログ




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学
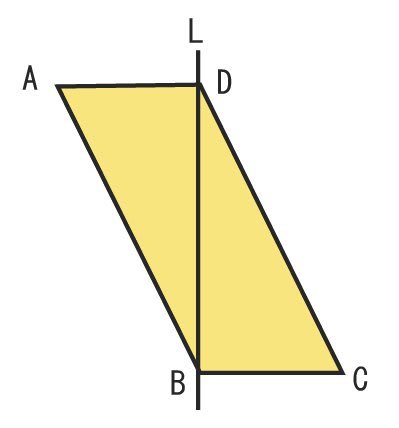



円錐を カット する 体積は どうなる 名寄 算数数学教室より



数学 三角錐の体積比を楽に求められる公式 受験の秒殺テク 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



Math 円錐 円錐台と面積比 体積比 働きアリ



円すい 算数星人のweb問題集 中学受験算数の問題に挑戦



Newみんなの算数講座104 プリン 中学受験の算数知恵宝庫



Math 円錐 円錐台と面積比 体積比 働きアリ The 2nd



円錐の表面積の求め方を解説 円錐の表面積の求め方は完全パターン化できる



直円錐の体積



中3数学相似の問題です 下の図で 円錐の底面を平行な高さで三等分してでき Yahoo 知恵袋



相似比と面積比と体積比の関係を解説 公式を使って面積や体積を求めよう




表面積と体積の比の問題 立体の相似比を出すのが一番最初だ 中学や高校の数学の計算問題



数学 三角錐の体積比を楽に求められる公式 受験の秒殺テク 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




中3数学 相似な図形の表面積比 体積比 映像授業のtry It トライイット



1



相似な図形 体積比 相似な図形に注目せよ 苦手な数学を簡単に




立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者



Math 円錐 円錐台と面積比 体積比 働きアリ



円錐と体積比 中学から数学だいすき



円錐や三角錐の体積比の求め方 相似比 辺の長さの比から計算 白丸くん



ピタゴラスイッチ 円錐 円柱 球体の体積比は Jyankquiz



誰か相似の体積比をわかりやすく説明お願いします Oc Ca 3 1となる Yahoo 知恵袋




円錐台の問題がわかりません 写真は円錐の上部を底面に平行な平面で切った円 Okwave




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




数学 三角錐の体積比を楽に求められる公式 受験の秒殺テク 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




相似と体積比 3 ネット塾
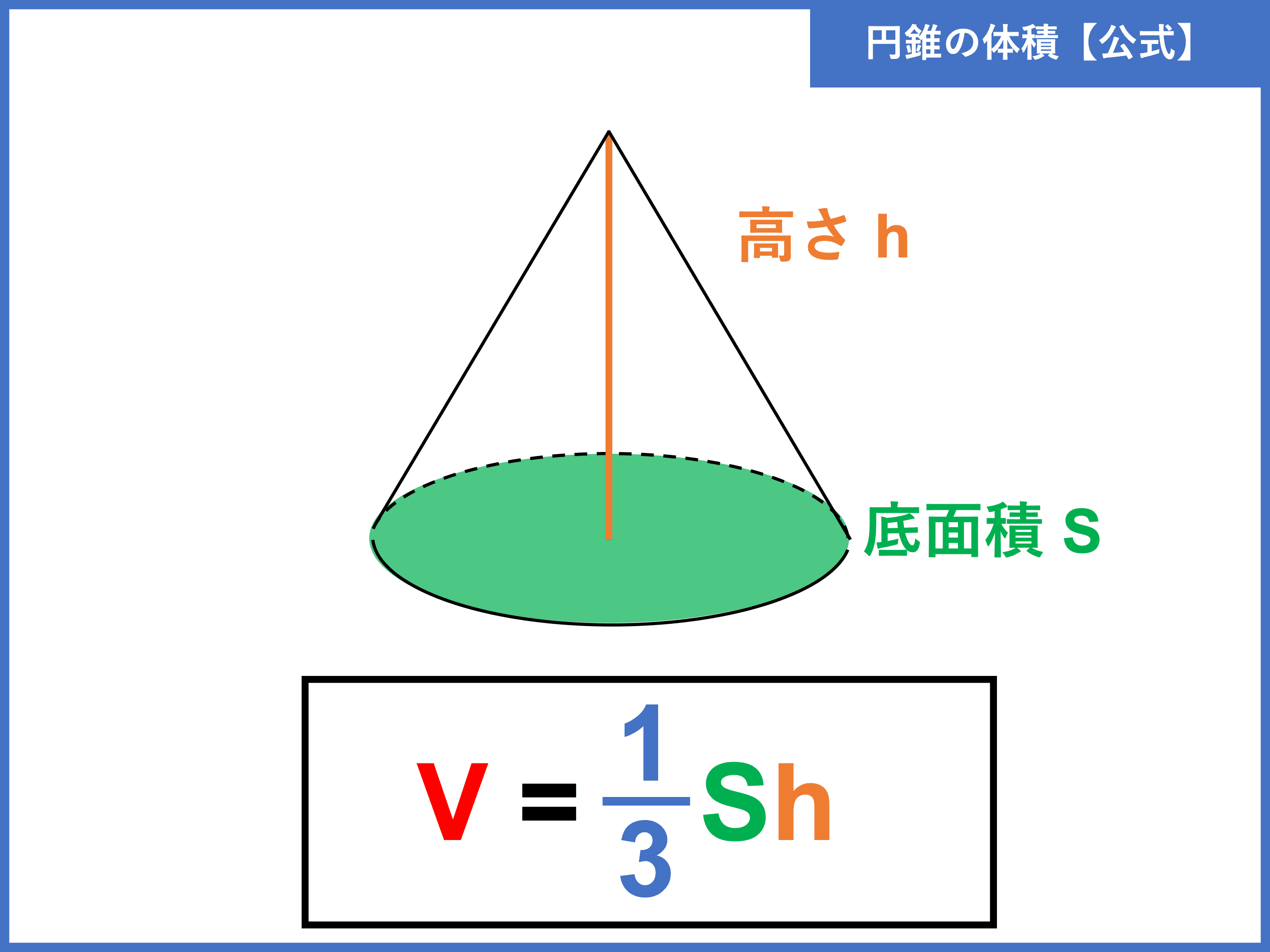



Hd限定円錐 体積 の 求め 方 ページを着色するだけ




中3数学 相似な図形の表面積比 体積比 練習編 映像授業のtry It トライイット
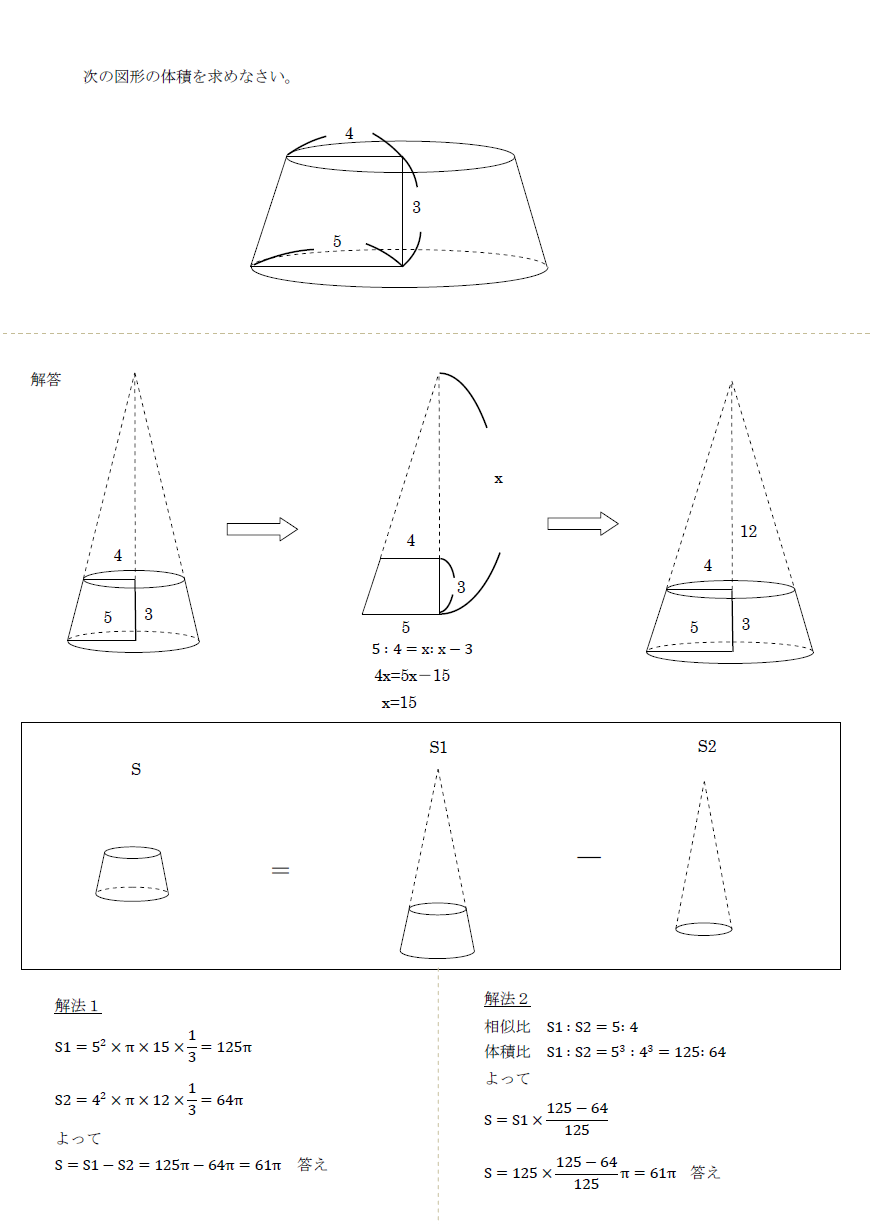



空間図形の体積 円錐台 の解法 中学 受験 定期試験 数学解き方集 裏技 解法
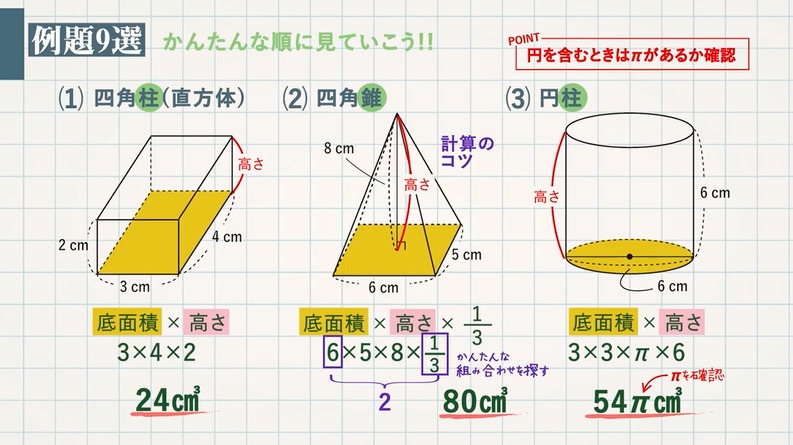



立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者




空間図形08 三角すいの体積比 Youtube



相似な立体 中学3年 数学クラブ




3分でわかる 相似比から体積の比 表面積比を求める公式 Qikeru 学びを楽しくわかりやすく




高校数学 立体 正四面体 直円錐 表面上の最短経路 受験の月




中学数学 円錐の表面積の求め方と公式 図たくさん なぜか分かる はかせちゃんの怪しい研究室




体積比の求め方が分かりません Clear




球の表面積と体積の公式 数学fun



立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者



1



中学数学 円すいに関する練習問題



1




中3 三角形の相似 円錐の体積比 日本語版 Youtube




空間図形の表面積比と体積比 数学i フリー教材開発コミュニティ Ftext




公式を図解 すい体の体積 円すいの表面積の求め方



Www Pref Osaka Lg Jp Attach 6629 Jmw 3b5 11 Pdf



0 件のコメント:
コメントを投稿