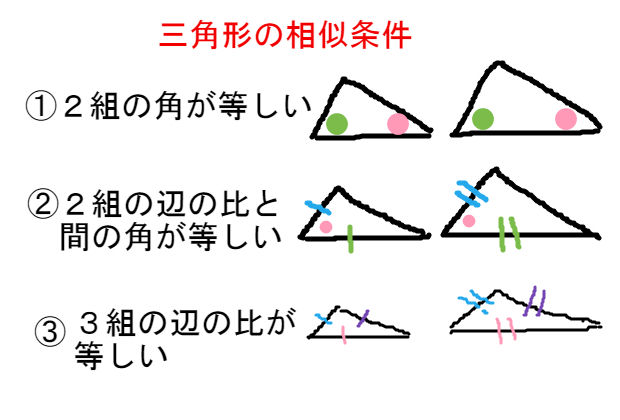
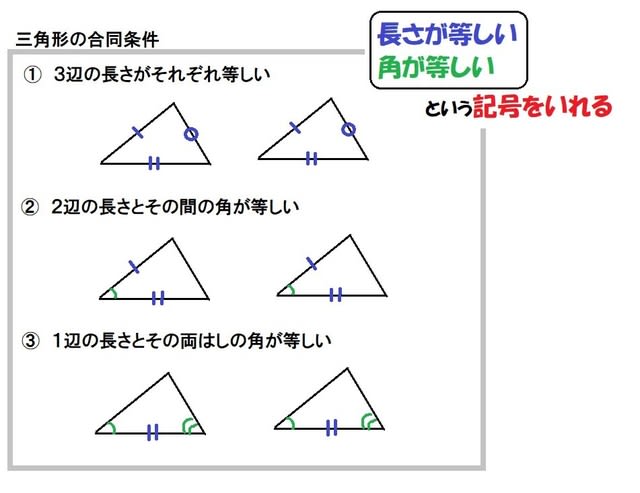
動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru合同に比べて、いろいろな問題のパターンがあるので、テストでも聞かれやすいです。それでは合同と相似をまとめます。 まとめ 合同は 形も大きさも同じ。 対応する角の大きさ、対応する辺の長さは等しい。 まとめ 相似は 形は同じ。大きさは違う。相似相似时行列式,秩,迹,特征多项式,特征子空间维数相等 n阶矩阵可对角化=>有特征向量构成的K n 的基 不同特征子空间线性无关 实对称矩阵正交相似于对角矩阵 对称矩阵合同于对角矩阵, 二次型等价于只含平方项的二次型 惯性定理

考研数学 令人头大的相似 合同 等价 复习经验 考研帮 Kaoyan Com
合同 相似 三角形
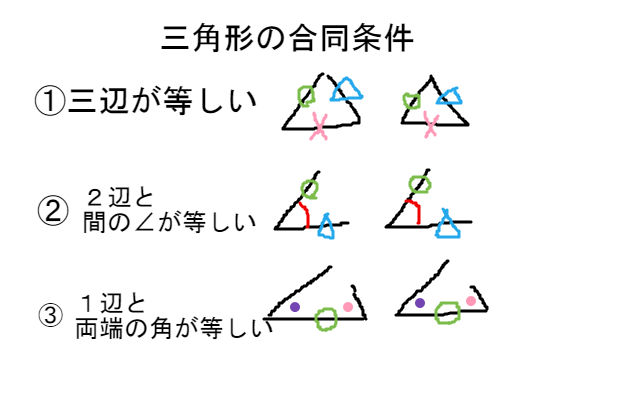
合同 相似 三角形- 合同条件と相似条件の似ているところと、違うところを中心に復習していくよ。 三角形の合同条件と相似条件を3つの種類にまとめてみた 三角形の合同条件と相似条件をうまく覚えるために、3つの種類に分類してみたよ。 3つの何かが等しい条件相似和合同的关系 : 相似是能找到一个p,使得p逆ap=b,此时我们称a和b相似合同是能找到一个p,使得p转ap=b,此时我们称a和b是合同的关系如果 p逆=p转,即a和b即是相似关系又是合同的关系,此时p是一个正交阵总的来说,相似不一定合同,合同不一定相似
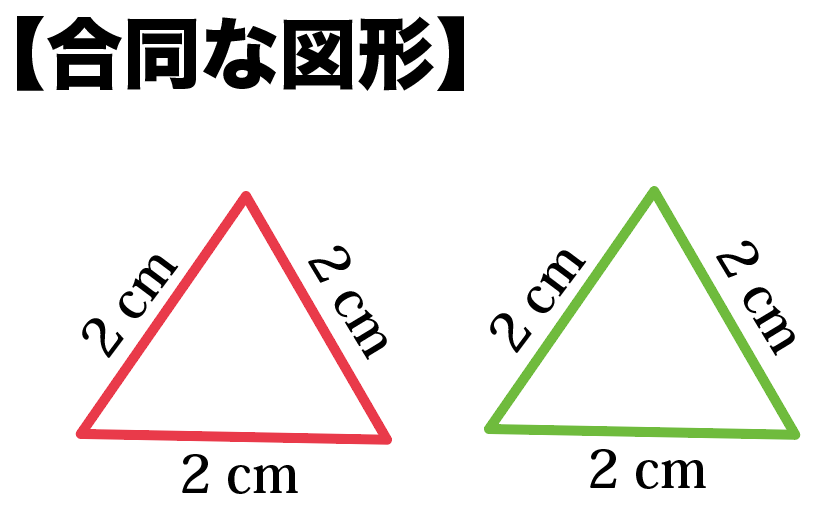



知っておきたい 相似と合同の3つの違い Qikeru 学びを楽しくわかりやすく
相似和合同的关系 —— 1、等价(只有秩相同)负惯性指数相同)–>相似(秩,正负惯性指数,特征值均相同),矩阵亲密关系的一步步深化2、相似矩阵必为等价矩阵,但等价矩阵未必为相似矩阵 ,pq=epq=e 的等价矩阵是相似矩阵3、合同矩阵必为等价矩阵,等价矩阵未必为合同矩阵,正惯性指数相同的等价矩阵是 等价、合同、相似、正交变换;二次型,正定,惯性指数 方阵的变换有以下几种: 等价变换:方阵A右乘一个满秩方阵P,左乘个满秩方阵Q,P和Q没有任何约束关系,这就是等价变换。 等价变换是保秩变换。 当对P和Q有一定约束时又有一些特殊的变换。 合同变换_____ 相似矩阵的特征植相同,特征植正负个数相同,惯性指数相同,故合同 矩阵合同和相似有关系吗 _____ 合同和相似对应的分类都是无限多种如果,你学过基数相关的知识,实际上他是连续统基数(这个基数是无穷基数)那么多种
合同的话,由于实对称阵的合同阵一定也是实对称阵,所以如果有两个矩阵相似但是一个是实对称阵一个不是,那他们必不可能合同 嗯 看来又翻车了 推不出相似,但是能推出相似于各自单项选择题 设方阵A与B相似,则()。 单项选择题 二次型f=xTAx的矩阵A的所有对角元为正是f为正定的()。 单项选择题 设3阶矩阵A的特征值为0,1,2,那么R(AE)R(A 单项选择题 下列矩阵中可对角化的是() 合同矩阵的性质相似矩阵与合同矩阵 要:矩阵的相似与矩阵的合同是线性代数中两个重要的概念对它们的定义如何?它们定义 中所表现出来的异同点作了简 单阐述二者都是针对方阵来说的,定义中都是要求存在一个可逆 矩阵,但一个是可逆矩阵的逆,一个是
合同矩阵,在 线性代数 , 特别 是 二次型 理论中,常常用到 矩阵 间的 合同关系 。 两个矩阵A和B是合同的,当且仅当存在一个 可逆矩阵 C,使得C T AC=B,则称方阵A合同于矩阵B。 中文名 合同矩阵 反身性 任意矩阵都与其自身合同; 对称性 A合同于B,则 若合同,保证了正、负系数的个数相同,此时虽然可以相似对角化,但各自具体的特征值不一定相同,所以推不出a、b相似。 例对角矩阵2E合同于单位矩阵 E,而 E 只能和 E 相似,显然2E不相似于E(因为特征值不同)。2つの図形 F と G が相似(そうじ、英 similar )であるとは、一方を適当に点スケール変換(拡大 (enlarging) または縮小 (shrinking))して他方と合同になる(すなわち、有限回の平行移動、回転移動、対称移動により重なる)ことである。 それらの「形」が等しいことであるとも言い換えられる。




合同相似素材图片 摄图新视界



把握住这两点实对称方阵的相似合同判断就没问题啦 线性代数系列篇7 实对称方阵的相似和合同 第五维教育
相似就是一个矩阵在同一空间中不同基之间的变换,而合同是欧式空间中不同基的度量矩阵之间的变换,由于基决定度量矩阵 (度量矩阵是对称正定的,且任意一组标准正交基的度量矩阵是E),而度量矩阵唯一决定内积 ( (α,β)=X^TAY=αβ^T),且正交即内积为0 (即⊥ 矩阵 合同,当且仅当 有相同的正惯性指数 Remark 相似关系保特征值 合同关系保正惯性指数 合同关系保正定型 实行正交变换时, ,此时所得的标准型才唯一 对于非正交变换,所得标准型不一定唯一 若 是实对称矩阵,则 既相似又合同于对角阵 { "score" , "words" { "word_1" "北京", "word_2" "上海" } } 上一篇 中文词向量表示 下一篇 中文DNN语言模型
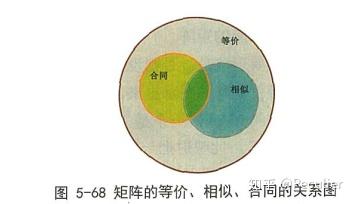



矩阵的等价 相似及合同 知乎
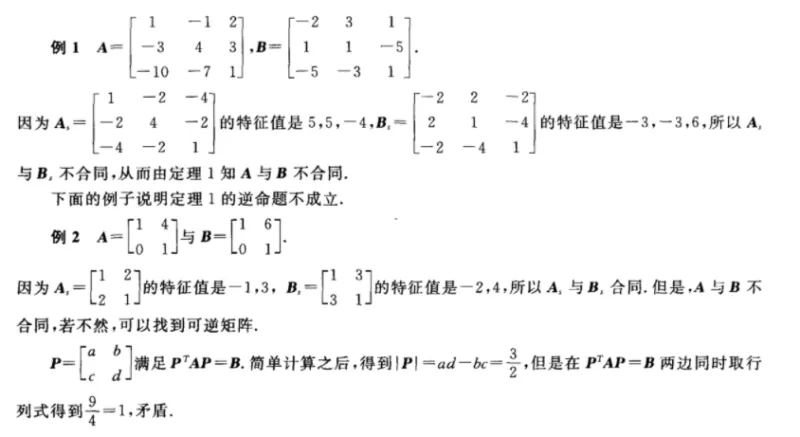



普通矩阵相似不一定合同 步行街主干道 虎扑社区
相似な2つの図形の対応する辺の長さの比を相似比といいます。 つまり、最初の方で説明した合同な図形は相対比が1:1の相似な図形と考えることもできます。 例題 例題1 下の図で、合同な三角形はどれ一番右は他のどれとも合同でも相似でもない。 注意すべき点は、図形の合同において位置や向きといった一部の性質・量は変わるが、 距離 や 角度 といった性質・量は変わらないということである。合同符號的歷史 萊布尼茲最先發明了相似與合同的符號 ,他使用波浪號( )來表示幾何形的相似,另在波浪號下方加上一條橫線( )來表示幾何形的合同。 十八世紀的數學家將相似符號( )與等號( = )結合在一起( ),更能表達出合同的意義,亦即相似與相等的重合概念。



合同范本



相似等价合同符号 等价相似合同的符号 符号大全
摘要: 考研数学里关于矩阵的相似、合同、等价的关系有时令大家头晕脑胀,就需要大家对它们的性质、定义要更加清楚,得分才不难。 接下来一起看看三者的纠缠吧。 关于矩阵的相似、合同、等价的关系 总结起来就是一句话 相似必合同,合同必等价 1、合同即特征值正负0个数分别相同; 2、相似,特征值相同且都可以对角化或者说特征值相同且都有n个线性无关特征向量; 3、等价,秩相等; 合同和相似是特殊的等价关系。 等价一般是指可以通过初等变换变成另一个,本质上只需要两个矩阵秩相同就可以签订的相似词 签定 签署 签订协议 合作协议 签订的协议 协议 订立 签订合约 意向协议 合作协议书 签定协议 签署协议 框架协议 相关协议 签订的合同 签属 签立 协议内容 签署合同 补充协议 意向协议书 合作合同 合作意向书 签订合同 协议书 合作框架协议 签有




线性代数学习笔记 第七十六讲 矩阵的合同 预见未来to50的专栏 Csdn博客 矩阵合同
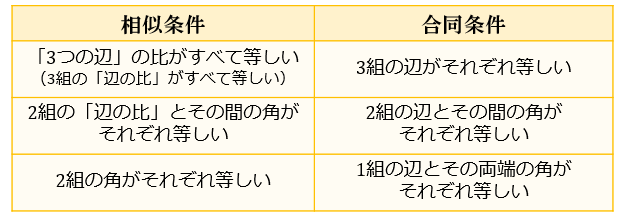



三角形の合同条件 相似条件と合同条件の違いとは アタリマエ
証明 (合同・相似)が苦手な人へ 教遊者 IC Channel 192K subscribers Subscribe 中2,中3,受験生平行と合同,三角形と四角形,相似「証明 (合同・相似)が苦手な人へ90%以上の証明に使えるテンプレートと素材まとめ」デジタル板書データ Watch later ④合同条件(または相似条件)の3つからどれが当てはまるか を探っていきます。 もし、そこで条件が揃っていれば証明は出来ます。 これで解けるのは教科書範囲の問題が多いです。 入試問題では条件が1つ足りないことがよくあります。 そうなった場合は、 相似P?1AP?B,P可逆 论文网怎么判断两个矩阵是合同的)有四个必要条件秩相同,特征值相同,特征多项式相同,行列 式相同,如何判断两个一般的矩阵是否相似,考研大纲并不要求, 但是如果A,B 相似于相同的对角阵,则由相似关系有传递性知A,B 相似 合同 (仅限于



物流图表 中美合同物流发展的相似与不同 合同物流 供应链 中国电子商务 美国 科技
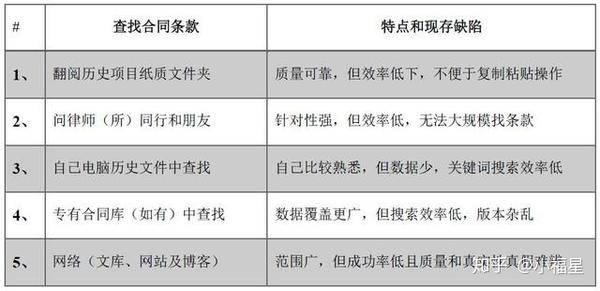



Ai方式极客搜索相似合同条款 即刻改变合同审查的姿势 知乎
两矩阵秩相等,则两矩阵等价 还有一个问题,若A,B均为n阶对称矩阵,且A与B的惯性指数相同,则A与B合同如果仅告诉了A 1年前 1个回答 矩阵等价、相似、合同"矩阵它有3种等价关系等价、相似、合同";这句话里,两个等价意思一样吗?如一样,感觉好怪,怎么理 1年練習プリントをダウンロード https//ecommonsbiz/wpcontent/uploads//12/DB127pdf 動画リンク 証明(合同・相似)が苦手な人へ90 答案 相似必然相抵, 合同必然相抵 ,但不一定相似, 反之均不然 特别,若 P P P 为正交矩阵,则 B = P T A P = P − 1 A P B= P^TAP=P^ {1}AP B = P T AP = P −1AP,此时合同与相似是一样的




矩阵的合同相似等价为什么这么定义呢 哔哩哔哩 Bilibili




保存版 三角形の合同条件と相似条件の6つのまとめ Qikeru 学びを楽しくわかりやすく
相似和合同不能互相推导 雨露学习互助 矩阵相似不合同,举反例谁能帮我举个例子啊,要2个矩阵相似,但是不合同的,实对称矩阵才有相似才合同。 相似和合同不能互相推导 这个不是相当容易的吗,A和B合同的必要条件是AA'和BB'合同 显然相似但不合同 矩阵的等价,合同,相似的联系与区别doc,目 录 摘 要 I 引言 1 1矩阵间的三种关系 1 11 矩阵的等价关系 1 12 矩阵的合同关系 2 13 矩阵的相似关系 2 2 矩阵的等价、合同和相似之间的联系 3 3矩阵的等价、合同和相似之间的区别 6 结束语 6 参考文献 6 1矩阵间的三种关系 11 矩阵的等价关系 1 两个矩阵等价 相似と合同の3つの違い 相似と合同の違いはつぎの3つかな。 3つもあるんだ! たいへん! ! ゆっくりみていけば大丈夫。 それじゃあいくよー! 違い1 「言葉の意味」




合同相似可逆等价矩阵的关系及性质 矩阵的三种 Quot 等价关系 Quot Dearyee的博客 Csdn博客




判断下列矩阵既相似又合同 知乎
在線性代數中,相似矩陣(英語: similar matrix )是指存在相似關係的矩陣。 相似關係是兩個矩陣之間的一種等價關係。 兩個n×n矩陣A與B為相似矩陣若且唯若存在一個n×n的可逆矩陣P,使得: = P被稱為矩陣A與B之間的相似轉換矩陣。 相似矩陣保留了矩陣的許多性質,因此許多對矩陣性質的研究可以 矩阵的相抵、合同、相似doc,莆田学院数学系 "高等代数选讲"课程论文 题目: 矩阵的相抵、合同、相似 一些关于这三种等价关系的联系、差别和不变量 姓名: 阮超英 学号: 数学系02级本科(1)班 05 年6月23日 矩阵的相抵、合同、相似 一些关于这三种等价关系的联系、差如何直观理解矩阵的"等价""相似""合同"及"二次 : 等价一般是指可以通过初等变换变成另一个,本质上只需要两个矩阵秩相同就可以了是个很宽泛的条件,应用不大a相似于b,是存在非异矩阵p,使得pap^1=b,这个是线性代数或者高等代数里面最重要的关系
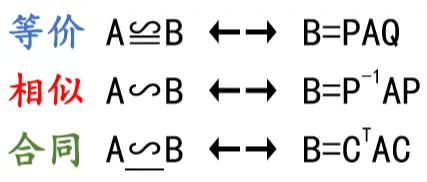



晕 矩阵等价 相似 合同 哔哩哔哩




判断下列矩阵既相似又合同 知乎
こんにちは、医学生gです。今回は 合同と相似 の話をしていきたいと思います。合同、相似は中学で登場して以降高校に入っても当たり前のように使う分野ですので、しっかりと理解していきましょう。 ここでは、できるだけゆる〜い言葉でふんわりと解説していくので、定義など正確



相似和合同的区别 合同和相似的区别 什么区别




考研数学 令人头大的相似 合同 等价 复习经验 考研帮 Kaoyan Com



矩阵的合同相似等价为什么这么定义呢 哔哩哔哩 Bilibili




惊人相似 合同2 0版本 这两家平台原来是一家




知っておきたい 相似と合同の3つの違い Qikeru 学びを楽しくわかりやすく



合同と相似の複合問題 制限3分 中学数学 理科 寺子屋塾の復習サイト



矩阵的合同 等价与相似的联系与区别下载 Word模板 爱问共享资料




第九章二次型研究对象 二次齐次多项式 1 也叫二次型 2 在数学和物理的许多分支都有重要应用 3 展现矩阵的无穷魅力




张宇数一四套卷第二套 虎扑




17考研数学 相似矩阵与合同矩阵的异同分析 文都考研网



13 选择题必考的三大关系 等价 相似 合同 哔哩哔哩 つロ干杯 Bilibili
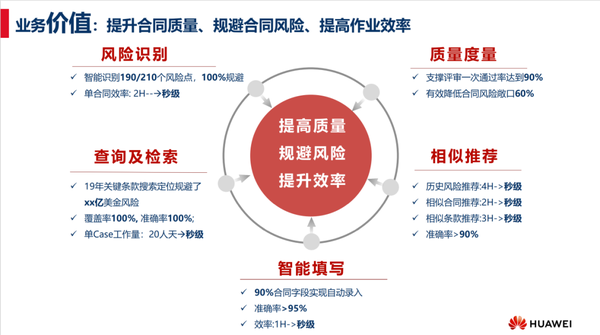



自从安上了 Ai 这些商务经理天天按时下班了 知乎




我在吃大西瓜呢




讲稿 矩阵合同相似下载 Word模板 爱问共享资料




书面签署商务交易合同相似素材图片 摄图新视界




线性代数学习笔记 第七十六讲 矩阵的合同 预见未来to50的专栏 Csdn博客 矩阵合同



合同と相似の複合問題 制限3分 中学数学 理科 寺子屋塾の復習サイト




15考研数学 矩阵的等价 相似 合同的联系及判定 文都考研网



还在傻傻分不清 矩阵的合同 等价和相似吗 哔哩哔哩 つロ干杯 Bilibili




数三刷题笔记 矩阵等价 相似 合同 正定的判定及性质 知乎




01年真题 两个矩阵合同相似问题 哔哩哔哩 Bilibili



矩阵合同相似 修订 下载 Word模板 爱问共享资料



初创型企业可以制定哪几项员工管理类合同 人事合同 E纸合约



上数学合同条件 ニスヌーピー壁紙




手机和手机合同相似素材图片 摄图新视界
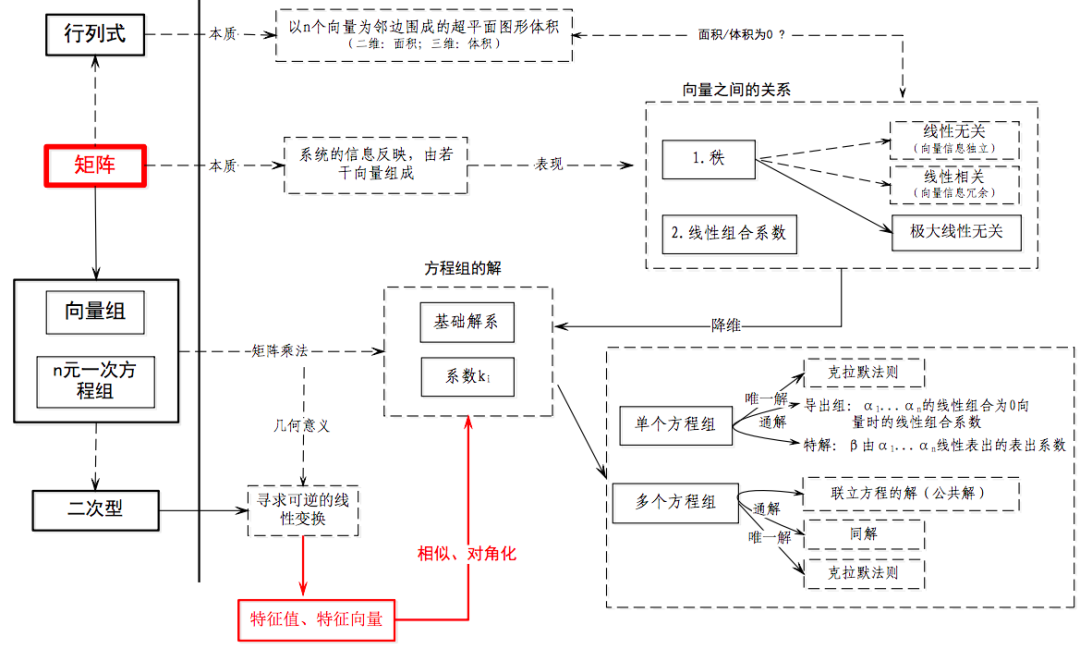



合同相似可逆等价矩阵的关系及性质 大一统 等价 相似 合同 买姑娘的小青蛙的博客 Csdn博客




三角形の相似条件と証明問題の解き方 数学fun
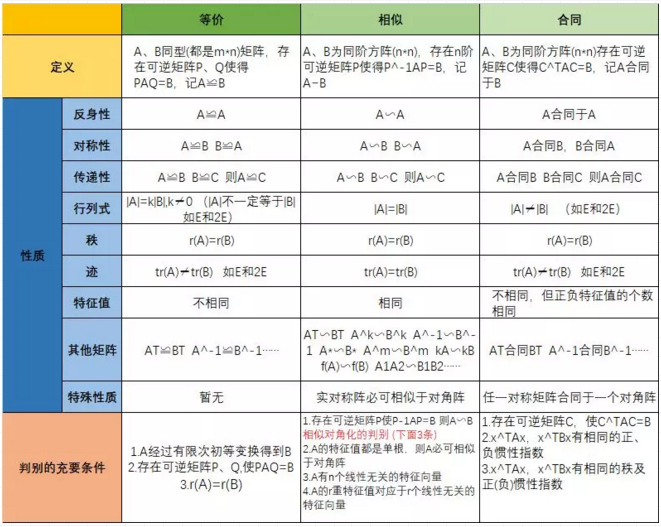



考研数学 令人头大的相似 合同 等价 复习经验 考研帮 Kaoyan Com



突破隔离 电子合同 的时代到来了 文章 专业研发 湖南人和人律师事务所 全国优秀律师事务所丨中国十佳ppp项目律师事务所丨alb中国十佳成长律所丨湖南省优秀律师事务所 人和人律师事务所官方网站




矩阵等价 相似 合同的判断 参考网




高校入試集中トレーニング合同 相似 高校入試集中トレーニング 13 数学 Amazon Com Books



矩阵的合同 等价与相似的联系与区别下载 Word模板 爱问共享资料



线性代数 第十五讲二次型的定义 合同与相似的关系 哔哩哔哩 Bilibili




张威老师 A是实对称阵 A与b相似 那么a与b合同吗 哔哩哔哩 Bilibili




商务合同相似素材图片 摄图新视界




合同 相似の英語をマスターしよう 英語独学マスター
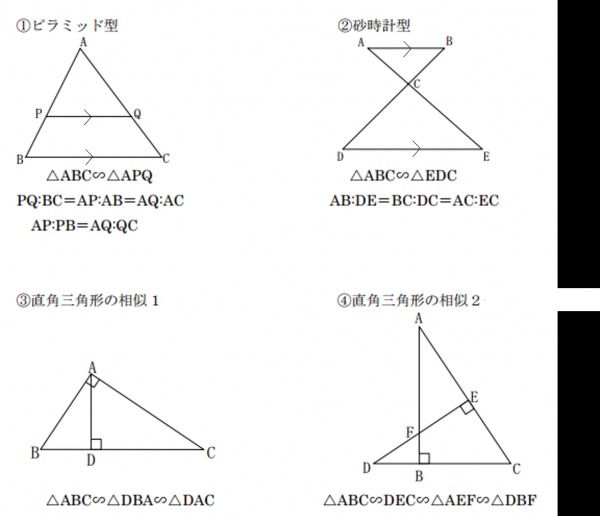



三角形の相似 合同条件 優技録




矩阵合同和矩阵相似的对比 柚子的行迹 Csdn博客




一图说明矩阵等价 相似 合同 程序员石磊 51cto博客




矩阵的等价 相似及合同 知乎




广告公司合同 协议 Word模板下载 合同 熊猫办公




031 矩阵关系专题之等价 相似 合同 线性代数系列结束 段智华的博客 Csdn博客 线性代数相似等价合同




21 二次型 合同关系 惯性指数 标准型 规范型 Xtax 知乎




矩阵等价 合同 相似的联系与区别 知乎



春季学期第七期学霸讲堂 等价 相似与合同的判定 哔哩哔哩 Bilibili
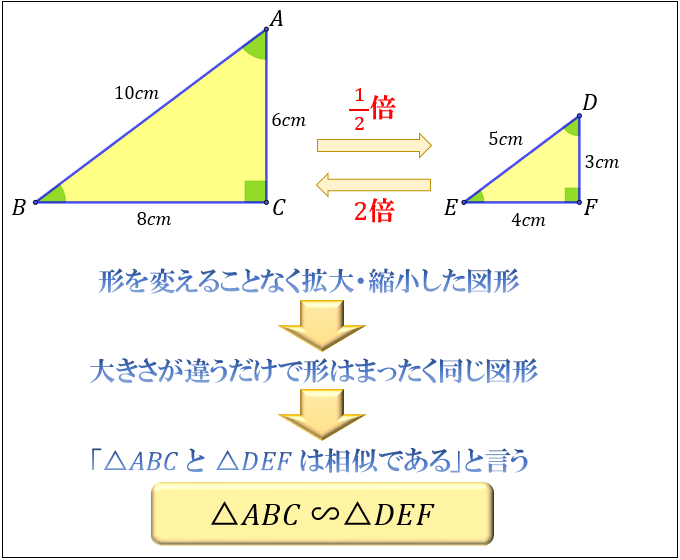



相似とは何か その意味 合同との違い 相似な図形が持つ性質について アタリマエ




讲稿 矩阵合同相似下载 Word模板 爱问共享资料




普通矩阵相似不一定合同 步行街主干道 虎扑社区
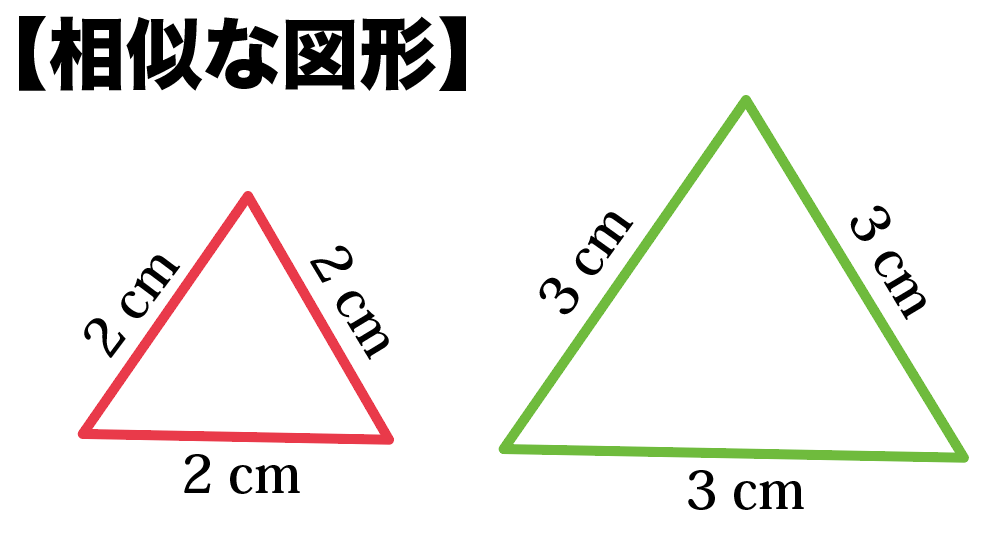



知っておきたい 相似と合同の3つの違い Qikeru 学びを楽しくわかりやすく




矩阵等价 相似 合同之间的区别和联系 百度知道
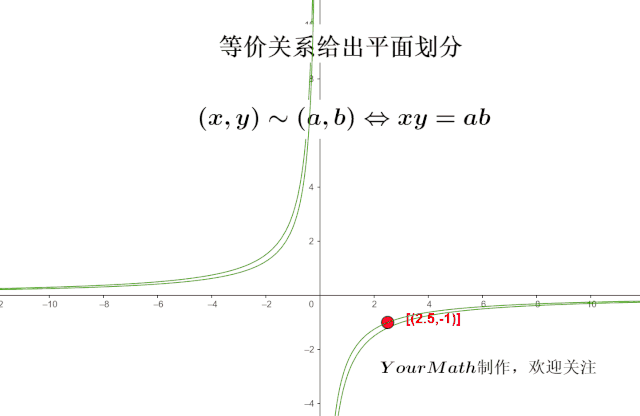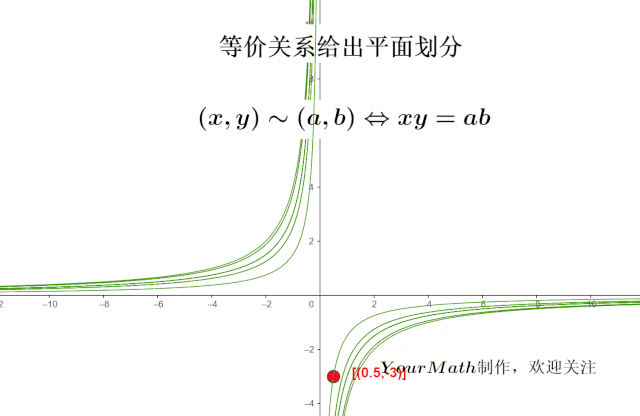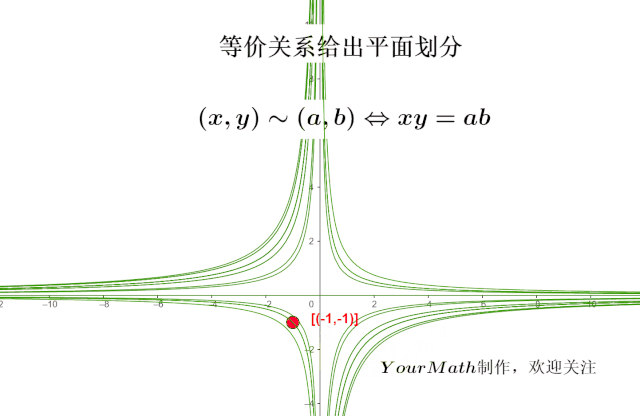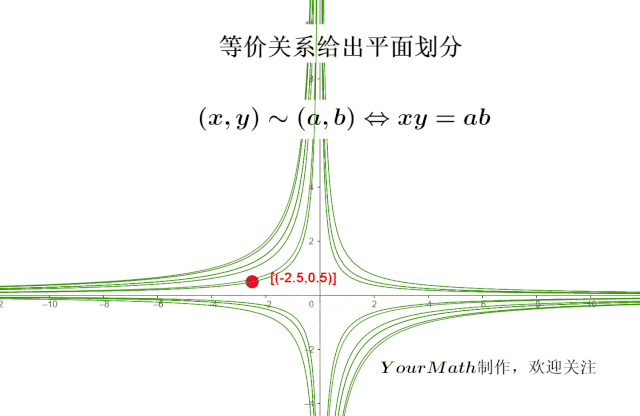



合同相似可逆等价矩阵的关系及性质 如何理解等价关系 Weixin 的博客 Csdn博客




矩阵迹的性质 矩阵等价 合同 相似的联系与区别 Weixin 的博客 Csdn博客




Ai方式极客搜索相似合同条款 即刻改变合同审查的姿势 知乎



法宝智能合同分析




晕 矩阵等价 相似 合同 哔哩哔哩



考研数学 常考题型 矩阵的相似 合同 等价 综合资讯 新东方在线移动版




合同相似可逆等价矩阵的关系及性质 大一统 等价 相似 合同 买姑娘的小青蛙的博客 Csdn博客



悟空问答 签订事业单位聘用合同这个属于事业编吗 职中有我的回答 0赞




合同矩阵 知乎




知っておきたい 相似と合同の3つの違い Qikeru 学びを楽しくわかりやすく
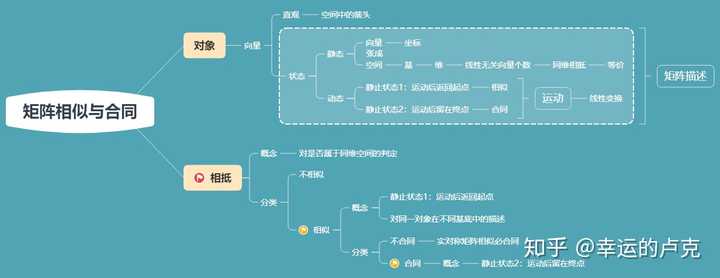



如何形象地理解矩阵的相似与合同 知乎



李林加一问 相似 合同于对角阵 有什么区别 哔哩哔哩 つロ干杯 Bilibili




我在吃大西瓜呢
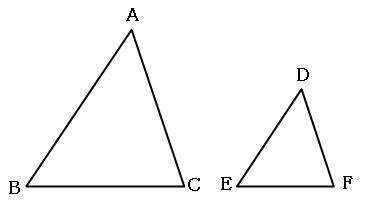



合同とは 相似とは



实对称方阵的相似合同判断 线性代数系列篇7 答案实对称方阵的相似和合同 雪花新闻




上数学合同条件 ニスヌーピー壁紙




晕 矩阵等价 相似 合同 哔哩哔哩




知っておきたい 相似と合同の3つの違い Qikeru 学びを楽しくわかりやすく




我在吃大西瓜呢



合同与相似的区别 相似与合同的联系和区别 什么区别



22考研数学 判断非对称矩阵的相似于合同问题 哔哩哔哩 Bilibili




网站设计合同相似素材图片 摄图新视界



Ig和rng的行为十分相似 却无人认为ig卡合同 只因没队要ning 战队




矩阵等价合同相似符号矩阵等价合同相似的符号分别是什么啊是这样的吗 我们的教材 代表相似 合同是图中的等价符号 那种对




17考研数学 矩阵合同与相似的典型题型分析 文都考研网



物流图表 中美合同物流发展的相似与不同 合同物流 供应链 中国电子商务 美国 科技




判断矩阵等价的方法 如何判断矩阵合同 相似 等价 三人行教育网 Www 3rxing Org




合同与相似概念区别下载 Word模板 爱问共享资料




卡通人物签名巨人合同相似素材图片 摄图新视界




15考研数学 矩阵的等价 相似 合同的联系及判定 文都考研网




17考研数学 相似矩阵与合同矩阵的异同分析 文都考研网



求相似矩阵的例题 西瓜视频搜索




魔鬼出示你签名的合同 相似素材图片 摄图新视界




Ai方式极客搜索相似合同条款 即刻改变合同审查的姿势 知乎



0 件のコメント:
コメントを投稿